题目大意是,构造一个n*n矩阵,由不同的正整数组成,使每行每列的数字积相等,还要求每个数字不能含有平方因子。
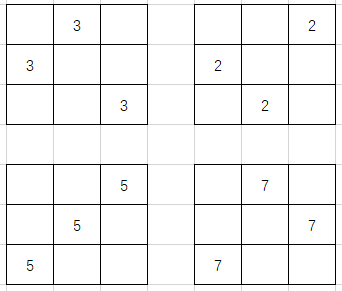
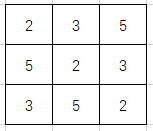
看完题目就能够想到这是一个构造题。搞一些质数行列错排一下对应位乘起来最后各个数字不一样就好。但问题是怎么排列能使每个数字不同。对题目给的样例分解一下会得到:
一开始想过按照错排的搜索顺序放置素数但好像素数好像不太够啊,又考虑随机放置素数错排,发现同样的数字就重排某个素数,但是太慢了要随机很久。
最后想到每个格子用两个素数组成,只要所有格子的素数对不同就好。
于是先搞出这样一个矩阵:
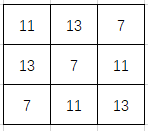
然后为了搭配一下再反着搞一下:
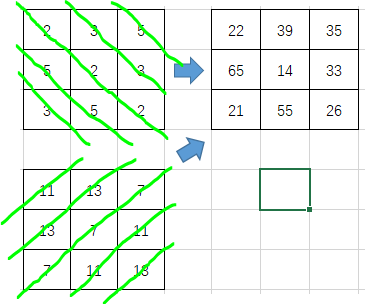
接着乘起来:
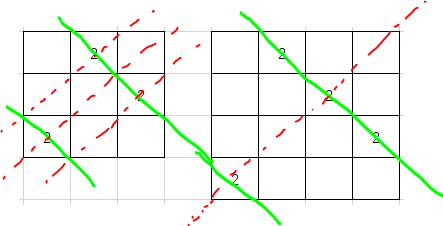
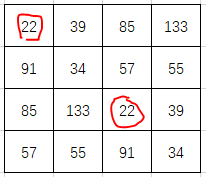
因为相同的数字都出现在斜线上,两个矩阵斜线方向不同,所以两个方向的斜线最多只能交出一个数,也就是说不同位置的数字应该不一样。看起来似乎做完了,但其实是有bug的。在n奇数时这样是没错的因为如下图,一个素数的两条斜线不会重叠,但是n偶数时会gg。
就是说,n为偶数时,一个数字会在它右下方n/2处重复。
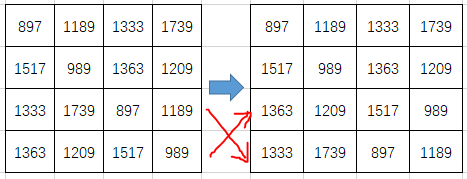
为了解决偶数的问题,我们可以再构造一个类似的矩阵,然后将它的下n/2半行,循环下移,这样不改变题目要求的行列积的性质,但是重复数字不会出现在原来的右下n/2处。
最后把这个矩阵和原先的到的矩阵对应位乘起来,因为两个满足条件的矩阵乘起来还是行列积相同的,两个矩阵数字重复的位置又不同,故乘起来后的矩阵的数字是各不相同的: